Melukis Grafik dengan Software Graph 4.3

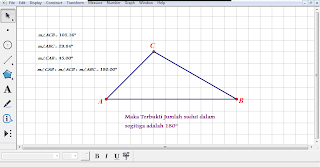
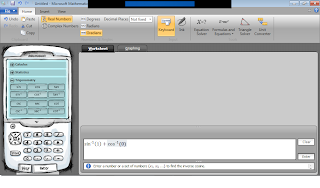
Saat ini, cukup banyak alat bantu berupa perangkat lunak (software) matematika yang dapat digunakan untuk menggambar grafik fungsi. Salah satu software matematika yang digunakan untuk menggambar grafik fungsi dan cukup populer adalah Graph. Salah satunya adalah Graph 4.3, berikut adalah beberapa contoh dari kegunaan Graph 4.3 :

Hal pertama yang harus dilakukan adalah, pastikan Program Aplikasi GRAPH ini ada dalam PC anda. Inilah tampilan awal dari aplikasi GRAPH.

Menggambar Elips

Langkah-langkah:

Pilih Menu Bar Function klik insert relation

Pada kotak dialog Insert relation, masukkan fungsi elips yang diinginkan

misalnya: x^2/9 + y^2/16 = 1, klik Ok

 Grafik-grafik dari persamaan elips pada pusat (0,0) adalah seperti gambar di bawah ini.

Grafik-grafik elips dengan pusat (a, b) adalah sebagai berikut.

Melukis parabola dan garis singgung parabola

Tampilan awal pada graph 4.3

Klik function pada toolbar lalu klik Insert relation atau tekan langsung tombol F6 pada keyboard.

Masukan persamaan parabola yang di inginkan , sebagai contoh y²=8x

 Lalu enter, maka akan terlihat gambar dari persamaan tersebut.

Setelah itu masukan persamaan garis yang membuktikan bahwa garis tersebut menyinggung parabola atau tidak.

Sama seperti memasukan persamaan parabola yaitu klik Insert Relation seperti berikut.

Lalu masukan persamaan garis yang di inginkan, contoh  y=x+2 sepesrti berikut.

 Lalu enter, maka akan terlihat gambar dari persamaan tersebut.

Menggambar Grafik Sinus dan Cosinus

Langkah-langkah:

Pilih Menu Bar Function klik Insert Function

Pada kotak dialog Insert relation, masukkan fungsi sinus yang diinginkan à klik OK.

Grafik-grafik dari persamaan fungsi sinus adalah seperti gambar di bawah ini.

Sin x

 

Sin x dan Cos x

Pilih Menu Bar Function klik Insert Shading

Lalu akan muncul gambar seperti ini

 Kemudian pada menu bar klik Calculate area, untu mengetahui Luas Daerah

Software Geometers Sketchpad untuk pembuktian-pembuktian Rumus

Software geometers sketchpad salah satu software untuk mempermudah guru dalam menjelaskan pembelajaran matematika khusunya pada bidang datar. Sketchpad merupakan software matematika dinamik yang interaktif.

Hal pertama yang harus dilakukan adalah, pastikan Program Aplikasi geometers sketchpad ada dalam PC anda. Inilah tampilan awal dari aplikasi geometers sketchpad.

Berikut penggunaan geometers sketchpad dalam pembuktikan rumus trapesium.

-Buatlah trapesium ABCD sama kaki

-Dengan kakinya di AD dan CB

-CD sejajar dengan EF, DE sejajar CF

-Panjang AE dengan FB sama panjang

-Hubungkan titik D ke titik F

Langkah-langkah        :

-Membuat titik point dengan point tool

-Sambungkan setiap titik dengan segment straightedge Tool

-Beri nama setiap titik dengan mengklik label point

-Beri nama pada garis DF (t), EF (a), AE dan FB (c)

Akan muncul seperti berikut :

 

-Ketik rumus trapesiumnya, karena Luas trapesium itu jumlah luas persegi panjang di tambah   dengan 2 kali luas segitiga maka didapat,

Dengan cara mengklik Text tool pada icon lalu klik di sembarang (klik 2x), setelah itu ketik rumus di atas.

Lalu, hitung panjang garis masing-masing AE, EF, BF, dan CE dengan klik segment garisnya lalu klik kanan pilih length

 

Selanjutnya , hitung luas trapesium sebelumnya klik polygon dan hubungkan titik-titik bidang datarnya

-hitunglah luas setiap bidang dengan klik kanan pilih area, 

-lalu pilih Number klik calculate dan jumlahkan semua area

 

Membuktikan Rumus Phytagoras

Langkah-langkah:

-Buat segitiga ABC menggunakan segment straightedge tool dan beri nama pada setiap titik-titik segitiga

-Klik text tool lalu klik 2x pada garis untuk mengganti nama garis, seperti berikut :

-Buat segitiga yang sama dengan rotasi 90⁰ searah jarum jam

-Hubungkan titik E atas dan garis B bawah dengan menggunakan segment straight tool

     -Pada segitiga atas beri nama L₁ menggunakan text tool lalu pilih symbolic notation dan pilih subscript

-beri nama L₁ pada segitiga bawah

-beri nama L₂ pada segitiga yang besa dengan cara yang sama

-masukkan rumus trapesium seperti pada gambar di bawah ini

     -Hitunglah dengan cara klik kanan lalu pilih area untuk mencari nilai a, b dan c. Lalu untuk membuktikan dalil phytagoras tersebut kita pilih menu number lalu pilih calculate

Membuktikan Jumlah Sudut Dalam Segitiga = 180⁰

Langkah-langkah:

-Buat segitiga ABC sembarang dengan menggunakan point tool lalu hubungkan setiap titik dengan segment straight tool dan beri nama pada setiap titik. seperti berikut :

    klik titik CAB kemudian klik measure pilih angle, lakukan juga pada sudut ACB, dan sudut ABC setelah ketiga sudut ditemukan klik number pilih calculate maka akan terbukti.

Jika ingin mengetahui luas segitiganya dengan cara klik polygon lalu klik pada titik-titiknya, klik kanan pilih area

    Terimakasih , semoga bermanfaat :-)

MICROSOFT MATHEMATICS (Pembahasan TRIGONOMETRI)

Kesempatan kali ini akan membahas bagaimana belajar Trigonometri menggunakan Microsoft Mathematics. Hal pertama yang harus dilakukan adalah, pastikan Program Microsoft Mathematics ada dalam PC anda.

Berikut tampilan layar awal pada Microsoft mathematics.

Pilih Trigonometry  pada kalkulator Microsoft.

Disini kita menggunakan fungsi Gradians.

Lalu klik sin

input [sin(90)+ lalu klik cos]

[sin(90)+cos(45)] lalu klik enter pada pojok kanan bawah.

Masih dengan menghitung. Sekarang akan menghitung menggunakan perpangkatan.

[sin^-1(1)+cos^-1(0)]. 

klik enter.

klik Calculus  pada kalkulator mincrosoft.

input penjumlahan integral dibawah ini.

untuk Penulisan pangkat tekan sift lalu pilih (^) sehingga muncul tanda panah ke atas lalu tekan angkat 2 untuk menunjukan pangkat à spasi makan akan muncul seperti berikut.

Pilih Enter.

pada kolom bawah output terdapat pilihan yang dapat kita pilih.

misalnya, klik plot this expression in 2D maka akan muncul seperti berikut.

atau kita dapat mengklik plot this expression in 3D.

Lalu Input penjumlahan integral dibawah ini.

Pilih Enter.

klik plot this expression in 2D.

atau mengklik plot this expression in 3D.

Sekarang, kita akan membandingkan menghitung dengan mengganti fungsi Degrees, Radians,dan Gradians pada menu.

Input fungsi trigonometri berikut.

Sin(90)+Cos(45)

 Hasil menggunakan fungsi Gradians. 

Hasil menggunakan fungsi Degrees.

Degrees adalah penggunaan derajat untuk pengukuran sudut dalam kalkulasi. (360 derajat)

Hasil menggunakan fungsi Radians.

Radians adalah penggunaan derajat dalam lingkaran untuk mengukur sudut dalam kalkulasi.
 (2 π rad)

 

Hasil dari ketiga fungsi diatas berbeda, dikarenakan pada fungsi Gradians, Degrees, dan Radians memiliki fungsi yang berbeda.

Pada perhitungan biasa, suatu penjumlahan pengurangan perkalian ataupun pembagian tidak akan mempengaruhi hasil dari operasi bilangan. Tetapi dalam perhitungan Trigonometri (sin, cos, tan, dkk), akan menemukan hasil yang berbeda pada penggunaan fungsi Gradians, Degrees, dan Radians.

Input fungsi trigonometri berikut.

Sin(90)+Cos^-1(30)

lalu enter.

g

Jawaban yang dihasilkan adalah indeterminate. Mengapa?

Karena Cos^-1(30) tidak terdefinisi. 

Sekian Terimakasih

Semoga bermanfaat ^_^9